![[자료구조] 시간 복잡도를 나타내는 BIG-O 표기법 - (3)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F0ap7y%2Fbtra8AiMKmi%2FNLKPKoGi14YCIROcxN6ev1%2Fimg.png)

목표
알고리즘 성능평가를 위한 시간 복잡도를 나타내는 BIG-O 표기법에 대해서 이해하도록 하겠습니다.
목차 클릭하면 해당 목차로 이동합니다.
개요
3번의 게시글에 걸쳐서 가상 컴퓨터, 시간 복잡도, BIG-O 표기법에 대해서 배우는 이유는 "알고리즘의 성능 평가" 때문입니다.
지금까지 알고리즘의 성능 평가를 하기 위한 환경, 방법에 대해서 배웠습니다.
이번 시간에는 알고리즘의 성능을 증가율 측면에서 바라보는 BIG-O 표기법에 대해서 배워보도록 하겠습니다.
시간 복잡도의 활용
BIG-O 표기법에 이해하기 전에 시간 복잡도를 활용해서 알고리즘의 성능 평가를 어떻게 하는지 알아야 합니다.
저희는 이전 게시글을 통해서 알고리즘을 보고 알고리즘의 수행시간 즉, 시간 복잡도를 계산할 수 있게 되었습니다.
그래서 ArrayMax, Sum1, Sum2라는 알고리즘의 시간 복잡도를 확인했었습니다.
이전 게시글 참고 : [자료구조] 알고리즘 성능평가를 위한 시간 복잡도 완벽히 이해하기! - (2)
각 알고리즘의 시간 복잡도는 다음과 같습니다.

이걸로 어떻게 알고리즘의 성능 평가를 할까요?
지금까지 배운건 최악의 입력에 대한 기본 연산 횟수만을 알 수 있습니다. 그럼 알고리즘의 성능 평가를 할 때 모든 경우의 수를 대입해야 할까요?
생각만 해봐도 상당히 까다로운데요. 당연히 일일이 대입하지 않습니다. 위에서 보는 시간 복잡도만 봐도 함수로 이루어진 것을 알 수 있습니다.
이 함수의 특징들을 통해서 각 알고리즘을 비교해서 다음과 같은 특징들을 알 수 있습니다.
① Sum1이 ArrayMax보다 2배 느리다.
→ 각 상수는 제외하고 2n과 4n 이기 때문에 2배 정도 차이가 난다.
② Sum2는 n < 5/3 일 때, Sum1보다 빠르다.
→ 두 알고리즘은 n이 5/3일 때 만나는데, n < 5/3 일 때 Sum2가 값이 더 크기 때문에 빠르다.
③ Sum2는 n > 5/3 일 때, 무조건 Sum1보다 느리다.
→ 반대로 n > 5/3 일 때, Sum2가 값이 더 작기 때문에 느리다.
④ Sum2는 모든 n에 대해서 ArrayMax보다 느리다.
→ 항상 Sum2는 ArrayMax보다 값이 작기 때문에 느리다.
사실 확인을 위해 시간 복잡도를 보기 좋게 그래프로 나타내보겠습니다.

파이썬의 matplotlib라는 라이브러리를 통해서 그래프로 표현했습니다.
실제로 Sum1과 Sum2가 5/3에서 만나는지, 교차하고 있는지 그래프를 확대해보도록 하겠습니다.

보시면 약 1.5보다 큰 값 (5/3 = 1.6666···)에서 두 그래프가 교차하는 모습을 확인할 수 있습니다.
이를 통해, 5/3보다 작은 값에서는 Sum1이 더 느리고, 큰 값에서는 빠르게 동작하는 것을 알 수 있습니다.
BIG-O 표기법이란?
ArrayMax, Sum1의 시간 복잡도는 최고차항이 n입니다. 따라서, 입력한 크기 n에 대해서 선형적으로 증가하는 모습을 확인할 수 있습니다.
반면, Sum2의 경우 최고차항이 n^2(n의 제곱)입니다. n에 대해서 제곱으로 증가하는 모습을 확인할 수 있습니다.
그럼 우리는 다음과 같은 사실을 깨달을 수 있습니다.
알고리즘 성능 평가를 위해서 일정 값이 중요한 것이 아니고, 입력한 크기 n이 커질 때, 수행 시간이 얼마나 증가하는지가 중요합니다.
함수값의 증가율이 계속 올라가면 기본 연산 횟수가 증가하면서 알고리즘의 성능이 저하되는 것을 확인하는 것이 목표입니다.
미적분 배울 때 다들 배우셨을 텐데, 함수의 증가율은 최고차항이 좌지우지합니다.
입력값이 커질수록 상수항들은 알고리즘의 기본 연산 횟수에 큰 영향을 미치지 못하는 것을 그래프에서 볼 수 있습니다.
그래서 다른 것들은 다 신경 쓰지 않고 최고차항만으로 시간 복잡도의 대략적인 형태를 나타낸 것을 BIG-O표기법이라고 합니다.
혹은, 근사적 표기법(Asymptotic Notation)이라고도 부릅니다.
BIG-O 표기법으로 나타내는 방법
그렇다면 BIG-O 표기법으로 어떻게 나타낼 수 있을까요? 그 방법은 다음과 같습니다.
1. n이 증가할 때 가장 빨리 증가하는 최고차항만 남기고 다른 항은 모두 생략한다.
2. 최고차항에 곱해진 상수도 생략한다. (최고차항의 계수도 생략한다.)
3. 남은 항에 O( ) 안에 넣어 표기한다.
한 문장으로 말하면 최고차항 빼고 다 생략하고, 최고차항의 계수도 빼고 O( ) 안에 넣는 것입니다.
다음 Sum2의 시간 복잡도를 BIG-O 표기법으로 나타내겠습니다.
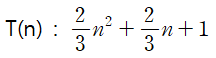
1. n이 증가할 때 가장 빨리 증가하는 최고차항만 남기고 다른 항은 모두 생략한다.
최고차항 빼고 다 생략하면 다음과 같습니다.
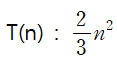
2. 최고차항에 곱해진 상수도 생략한다. (최고차항의 계수도 생략한다.)
최고차항의 계수도 생략하면 다음과 같습니다.
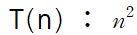
3. 남은 항에 O( ) 안에 넣어 표기한다.
이걸 O( ) 안에 넣어 표기하면 Sum2의 BIG-O표기법으로 나타낸 시간 복잡도가 나옵니다,

같은 방법으로 ArrayMax, Sum1의 시간 복잡도를 BIG-O 표기법으로 나타내면 다음과 같습니다.
| 알고리즘 이름 | 시간 복잡도 T(n) | BIG-O 표기법 |
| ArrayMax | 2n-1 | O(n) |
| Sum1 | 4n+1 | O(n) |
분명 다른 알고리즘임에도 불구하고 BIG-O로 나타내면 O(n)으로 같습니다.
위에서 2배 차이 난다고 해놓고 이렇게 같다고 해도 될까요?
BIG-O 표기법은 증가율 측면에서 표기하는 것이기 때문에 크게 보면 같은 알고리즘이라고 할 수 있습니다.
O(n^2)인 Sum2는 O(n)인 Sum1, ArrayMax보다 빠르게 증가하기 때문에 비교적 안좋은 알고리즘이라고 평가할 수 있습니다.
다양한 BIG-O 표기법
다른 알고리즘을 확인하면서 다른 경우에는 어떻게 나타내는지 확인해보겠습니다.
def increment_one(a):
return a+1입력값으로 a가 들어오면 1을 더해서 리턴해주는 알고리즘입니다.
시간 복잡도 T(n) = 1 입니다. 이런 경우에는 최고차항이 n^0 입니다. BIG-O 표기법으로 나타내면 O(1)입니다.
정말 1번 한다는 뜻이 아니고, 어떠한 입력이 들어와도 연산 횟수가 일정하면 O(1)과 같이 나타냅니다.
def number_of_bits(n):
count=0
while n>0:
n=n//2
count+=1
return count입력값 n이 들어오면 2로 나눈 몫을 n에 대입하는데, 몇 번 할 수 있는지 count로 세서 return하는 알고리즘입니다.
예를 들어, n=8이라면, n은 반복문을 거칠 때마다 8 → 4 → 2 → 1 → 0 순으로 바뀌고 4를 반환할 것입니다.
반복문 한 번 돌 때마다, n의 값은 n/2 → n/2^2 → n/2^3 → n/2^4 순으로 바뀔 것입니다.
2^count까지 가야 반복문이 끝납니다. 이 말은 반복문을 count번 해야 연산이 끝난다는 뜻입니다.
식으로 나타내면 다음과 같습니다.
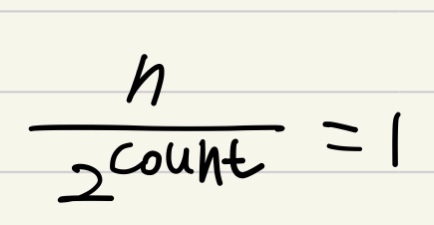
이걸 n에 대해서 정리하면 다음과 같습니다.
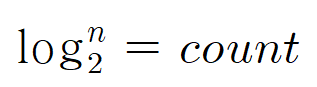
반복문은 log2에 n번 돈다는 것을 알 수 있습니다.
시간 복잡도는 다음과 같습니다.
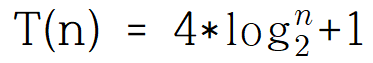
BIG-O 표기법으로 나타내려면, 최고차항 빼고 다 생략하고, 최고차항의 계수도 생략하라 했죠? 그럼 다음과 같이 나타낼 수 있습니다.
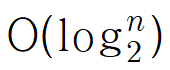
그래프로 확인해볼까요?

로그함수는 일차함수보다 증가율이 낮기 때문에 기본 연산 횟수가 더 적은 것을 확인할 수 있습니다.
따라서, 일차함수보다 좋은 알고리즘이라고 평가할 수 있는 것입니다.
BIG-O 시간 복잡도 그래프
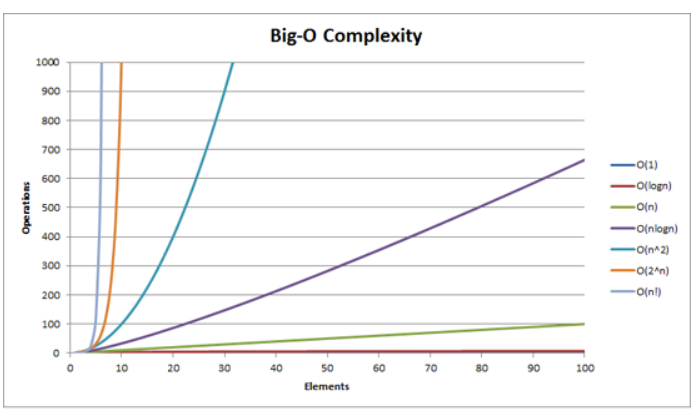
각 함수에 따른 시간 복잡도 그래프입니다.
증가율이 높을수록 입력 값이 커지면 기본 연산 횟수가 급격하게 증가합니다.
정리
이렇게 시간 복잡도와 BIG-O표기법에 대해서 알아봤습니다.
BIG-O 표기법은 최고차항을 제외한 항들을 생략하고 최고차항의 계수를 생략해서 O( ) 의 형태로 표기하는 것입니다.
BIG-O표기법으로 나타낸 시간 복잡도를 통해서 입력 값 n이 커질수록 알고리즘의 기본 연산 횟수가 얼마나 커지는지 알 수 있습니다.
다음 포스팅에서는 피보나치 수열을 통해서 O(2^n)과 같은 형태들을 살펴보고 알고리즘 성능 평가 파트를 마무리하도록 하겠습니다.
*한국외대 신찬수 교수님의 Data Structures with Python 강의를 참고하여 포스팅하였습니다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 순차적 자료구조, 배열과 리스트의 이해 (0) | 2021.08.10 |
|---|---|
| [자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기 (1) | 2021.08.03 |
| [자료구조] 알고리즘 성능평가를 위한 시간 복잡도 완벽히 이해하기! - (2) (1) | 2021.07.28 |
| [자료구조] 가상 컴퓨터(Virtual machine) 과 시간 복잡도(Time Complexity) - (1) (0) | 2021.07.26 |
| [자료구조] 최초의 알고리즘, 최대 공약수(GCD) 계산 알고리즘, 유클리드 호제법 (0) | 2021.07.16 |
![[자료구조] 순차적 자료구조, 배열과 리스트의 이해](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdBOj7d%2FbtrbCt5y8tl%2Fw8obdMKZDYwYE5rkZkRA81%2Fimg.png)
![[자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fd5OYJm%2FbtraWvwiTlx%2F6k2TReYFOkcHGhkTM6np90%2Fimg.png)
![[자료구조] 알고리즘 성능평가를 위한 시간 복잡도 완벽히 이해하기! - (2)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcwjCNA%2FbtraGG6gLWI%2FQR6ZXbskiELd3CV9dHK5K1%2Fimg.png)
![[자료구조] 가상 컴퓨터(Virtual machine) 과 시간 복잡도(Time Complexity) - (1)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4ToiJ%2FbtrazMx5Vwj%2F60TNfZ0GDE6sGfoTK88Lz0%2Fimg.png)