![[자료구조] 알고리즘 성능평가를 위한 시간 복잡도 완벽히 이해하기! - (2)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcwjCNA%2FbtraGG6gLWI%2FQR6ZXbskiELd3CV9dHK5K1%2Fimg.png)

목표
예시를 통해서 시간 복잡도에 대한 개념을 이해하도록 하겠습니다.
목차 클릭하면 해당 목차로 이동합니다.
개요
저번 포스팅에서 알고리즘의 성능 평가를 위해서 시간 복잡도(Time Complexity)라는 개념을 이용한다고 했습니다.
사람들마다 H/W, S/W 환경이 다르기 때문에 가상 컴퓨터(Virtual Machine)에서 가상 언어로 이루어진 가상 코드를 사용해서 알고리즘의 성능을 평가합니다. 포스팅 마지막에 가상 코드의 예시를 확인하면서 마무리했는데요.
이번 포스팅에서는 마지막에 확인한 코드를 보면서 시간 복잡도를 이해하는 시간을 갖겠습니다.
예시로 이해하는 시간 복잡도
알고리즘의 성능 평가는 알고리즘의 수행 시간을 비교해서 진행됩니다. 결과값을 얻는 데까지 알고리즘 수행 시간이 얼마나 걸리는지 확인하는 것입니다. 자세한 내용은 예제를 보면서 확인하도록 하겠습니다.
algorithm ArrayMax(A,n):
currentMax = A[0]············(ㄱ)
for i = 1 to n-1 do···········(ㄴ)
if currentMax < A[i]:········(ㄷ)
currentMax = A[i]········(ㄹ)
return currentMax저번 포스팅에서 본 ArrayMax라는 함수입니다.
언뜻 봐도 n개의 정수를 갖는 배열 A의 최대값을 currentMax에 저장하고 있다가 리턴하는 것으로 보입니다.
입력값(Input)과 출력값(Output)을 나누면 다음과 같습니다.
입력값 : n개의 정수를 갖는 배열 A
출력값 : A의 수 중에서 가장 큰 값
보시면 출력값은 정해져 있습니다. 입력된 A의 숫자 중에서 가장 큰 수를 리턴하면 됩니다. 반면, 입력값은 어떤 것이 들어올지 알 수 없습니다. 몇 개의 정수를 가진 배열이 입력될지, 배열의 숫자는 어떤 것이 들어갈지 확신할 수 없습니다. 예를 들어, n=3 , n=5, n=100, n=2438··· 어떤 숫자가 들어올지 예상할 수 없습니다.
또 n=3 일 때, A=[1,2,3], A=[3,2,1] / A=[2,-5,99] ··· 처럼 어떤 숫자가 배열 안에 들어있을지 알 수 없습니다.
이렇게 뭐가 어떻게 들어올지 모르기 때문에 때마다 단위 시간이 달라집니다. 입력값에 대해서 알고리즘의 성능을 평가하려면 일반적인 식이 필요합니다. 이에 대한 두 가지 방법을 제시하도록 하겠습니다.
입력값에 대한 알고리즘의 성능 평가를 위한 시간 복잡도 측정 방법
1. 모든 입력에 대해 기본 연산 수를 더해서 평균을 낸다.
2. 가장 안 좋은 입력(worstcase input)에 대한 기본 연산 횟수를 측정한다.(Worstcase Time Complexity)
기본 연산은 가상 컴퓨터(Virtual Machine) 위에서 1 단위 시간 동안 할 수 있는 연산을 뜻합니다. (이전 포스팅 이동)
이상적인 방법은 평균을 내는 방법입니다. 하지만, 예제에서 본 것처럼 모든 입력에 대한 평균을 내는 것은 현실적으로 불가능합니다. 그래서 알고리즘의 성능 평가는 대부분 2번, Worstcase Time Complexity를 이용합니다.
어떤 입력이 들어와도 이 WTC보단 수행 시간이 적기 때문에 믿을 수 있습니다.
그래서 일반적으로 알고리즘 수행 시간은 최악의 입력에 대한 기본 연산 횟수를 뜻합니다.
그렇다면 이번 예시에서 제일 Worstcase는 어떤 입력일까요?
아무래도 가장 안 좋은 상황은 기본 연산 횟수가 제일 많은 상황입니다. A=[4,3,2,1,···]과 같이 계속 줄어들면
0번째 인덱스가 가장 크기 때문에 (ㄹ)번 문장을 실행하지 않게 됩니다.
반면, A=[1,2,3,4,···]와 같이 계속 커지게 된다면 (ㄹ)번 문장을 계속해서 실행해야 합니다.
(ㄹ)번 문장을 실행한다는 것은 대입 연산을 한번 더 해야 하고 알고리즘 수행 시간이 증가하게 됩니다.
시간 복잡도 계산
이제 시간 복잡도를 계산해보도록 하겠습니다.
예를 들어, n=5이고 A=[3,-1,9,2,12]라고 가정해보겠습니다.
0번째 인덱스 3은 currentMax에 저장되면서 대입 연산을 합니다. (1회)
currentMax와 1번째 인덱스 -1을 비교하면서 비교 연산을 합니다. (2회) -1이 작으니 (ㄹ) 문장을 건너뜁니다.
currentMax와 9를 비교 연산(3회)을 하고 currentMax에 9를 대입 연산을 합니다.(4회)
다시 currentMax와 2의 비교 연산을 합니다. (5회) 2가 더 작기 때문에 (ㄹ)문장을 건너뜁니다.
currentMax와 12의 비교 연산(6회)을 하고 currentMax에 12의 대입 연산을 진행합니다.(7회)
이렇게 총 7회의 기본 연산을 진행하는 것을 확인할 수 있습니다. (반복문 제외)
모든 입력값에 대한 시간 복잡도는 일반적으로 T(n)으로 표기합니다.
Worstcase로 시간 복잡도를 측정하기 때문에 (ㄹ)문장을 계속해서 실행한다고 생각하겠습니다.
반복문 안 (ㄷ), (ㄹ) 문장을 보면, (ㄷ)문장에서 비교 연산 1회, (ㄹ)문장에서 대입 연산 1회를 실행합니다.
(ㄴ)문장에서 for문은 1 ~ n-1까지 총 n-1 회 실행하게 됩니다.
따라서, 시간 복잡도는 (ㄷ), (ㄹ) 문장 2회 * 반복문 n-1회 → 2(n-1) = 2n-2 = T(n)입니다.
맞을까요?
아니요. 지금 (ㄱ)문장을 생각하지 않았습니다. (ㄱ)문장에서 currentMax에 A[0]을 대입하는 대입 연산을 빼먹었습니다. 이렇게 처음 대입연산을 빼먹지 않도록 주의해야 합니다!
따라서, 시간 복잡도 T(n)=2n-1 이 됩니다. 예를 들어, n=6이라면, T(6) = 2*6 - 1 = 11이 됩니다.
최악의 입력(배열의 숫자가 계속 커지는 경우)일 때, n이 6이라면 기본 연산 횟수는 11번이라는 뜻입니다.
다양한 함수로 완벽하게 이해하기
다양한 함수의 시간 복잡도를 계산하면서 완벽하게 이해하고 넘어가도록 하겠습니다.
예시 1) sum1 함수
algorithm sum1(A,n):
sum=0··············(ㄱ)
for i=0 to n-1 do········(ㄴ)
if A[i]%2 == 0:···· ··(ㄷ)
sum+=A[i]········(ㄹ)
return sum두 번째 예제인 sum1 함수입니다. 보아하니, 짝수를 더해서 리턴하는 함수입니다.
이 함수의 시간 복잡도는 어떻게 될까요?
우선, 시간 복잡도는 worstcase를 기준으로 기본 연산 횟수를 계산해야 합니다.
이는 알고리즘의 수행 시간을 뜻한다고 적었습니다. 그렇다면 worstcase는 어떤 경우일까요?
sum1 함수의 worstcase는 배열 A의 모든 값이 짝수인 경우입니다.
모든 값이 짝수라면, (ㄹ)문장을 항상 실행해야 하기 때문입니다.
모든 값이 짝수라고 가정하고 시간 복잡도를 계산하도록 하겠습니다.
(ㄱ)문장에서 sum의 초기값 0을 넣어주는 대입 연산을 합니다. (1회)
(ㄴ)문장에서 반복문 n번 반복합니다.
(ㄷ)문장에서 A[i]%2(산술연산)을 해서 0과 비교하는 비교 연산을 합니다. (2회)
(ㄹ)문장에서 sum+=A[i] 는 sum = sum + A[i]으로 바꿔서 쓸 수 있습니다. 이렇게 보면 산술 연산(+)과
대입 연산(=)을 진행하는 것을 알 수 있습니다. (2회)
반복문 안에서 (ㄷ), (ㄹ) 문장을 진행하기 때문에 n * (2+2)를 하고, (ㄱ)문장의 1회를 더해주면 됩니다.
그래서 시간 복잡도는 T(n) = 4n + 1 입니다.
예시 2) sum2 함수
algorithm sum2(A,n):
sum=0························(ㄱ)
for i=0 to n-1 do············(ㄴ)
for j=i to n-1 do········(ㄷ)
sum+=A[i]*A[j]·······(ㄹ)
return sum다음은 sum2 함수입니다. 이중 for문이 앞서 본 2개의 예시와는 다릅니다.
이렇게 반복문이 중첩되어 있으면 어떻게 계산해야 할까요?
이번 예시에서는 첫 번째 반복문에서 따로 연산을 하는 것 없이 바로 두 번째 반복문으로 진입합니다. 그래서 i의 값보다는 j의 값을 알아야 시간 복잡도를 계산할 수 있습니다.
반복문이 중첩되어 있어도 우리가 생각해야 할 것은 "반복 연산을 몇 번 실행해야 하는가?"입니다.
이를 위해서 첫 번째 반복문 i와 두 번째 반복문 j의 관계를 먼저 살펴봐야 합니다.
| i | j |
| 0 | n |
| 1 | n-1 |
| 2 | n-2 |
| ··· | ··· |
| n-1 | 1 |
i의 값에 따른 j의 값을 알 수 있습니다.(반복문이 몇 번 도는지)
그렇다면 j의 경우의 수를 모두 더하면 기본 연산이 있는 반복문이 몇 번 진행되는지 알 수 있겠죠?
1 + 2 + 3 + 4 + ··· + n-1 + n 입니다. 등차수열의 합 공식을 사용하면 n(n-1)/2 입니다.
따라서, 반복 연산은 n(n-1)/2번만큼 실행합니다.
반복문 안에 있는 (ㄹ)문장은 sum+=A[i]*A[j] 이고, 풀어쓰면 sum = sum + A[i]*A[j]입니다.
대입 연산 1회, 산술 연산 2회(+,*)로 총 3회 연산을 진행합니다.
(ㄱ)문장의 처음 대입 연산 1회까지, 이 예시의 시간 복잡도는 다음과 같습니다.
T(n) = n(n+1)/2 *3 + 1 입니다. ( 3/2n^2 + 3/2n + 1)
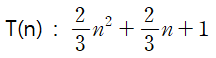
만약, 첫 번째 반복문 안에 추가적인 연산이 있고 중첩된 반복문이 있었다면 i를 이용한 추가적인 계산이
필요했을 것입니다.
정리
이렇게 3개의 예시를 보면서 시간 복잡도에 대한 개념을 익혔습니다.
요약하면, 알고리즘의 성능 평가를 위해서는 시간 복잡도라는 개념을 사용합니다. 시간 복잡도란, 알고리즘의 수행 시간을 측정하는 것으로, 최악의 입력에 대한 기본 연산 횟수를 뜻합니다. 또한, 시간 복잡도는 가상 컴퓨터 위에서 가상 코드를 활용해서 구할 수 있고 T(n)처럼 함수의 모양으로 나타낼 수 있습니다.
각 예시의 시간 복잡도는 2n-1, 4n+1, 3/2n^2 - 3/2n + 1이었습니다.
1, 2번째는 n이 1차 식이고, 3번째 예시는 n이 2차식입니다. 시간 복잡도의 최고차항에 따라서 특징들이 있습니다.
아무래도 최고차항이 크다면 n의 크기가 커질수록 시간 복잡도가 가파르게 상승하겠죠?
이와 같은 특징들을 다음 포스팅에서 정리하도록 하겠습니다. 또한, BIG-O라는 시간 복잡도 표기법에 대해서 알아보겠습니다.
*한국외대 신찬수 교수님의 Data Structures with Python 강의를 참고하여 포스팅하였습니다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 순차적 자료구조, 배열과 리스트의 이해 (0) | 2021.08.10 |
|---|---|
| [자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기 (1) | 2021.08.03 |
| [자료구조] 시간 복잡도를 나타내는 BIG-O 표기법 - (3) (0) | 2021.08.02 |
| [자료구조] 가상 컴퓨터(Virtual machine) 과 시간 복잡도(Time Complexity) - (1) (0) | 2021.07.26 |
| [자료구조] 최초의 알고리즘, 최대 공약수(GCD) 계산 알고리즘, 유클리드 호제법 (0) | 2021.07.16 |
![[자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fd5OYJm%2FbtraWvwiTlx%2F6k2TReYFOkcHGhkTM6np90%2Fimg.png)
![[자료구조] 시간 복잡도를 나타내는 BIG-O 표기법 - (3)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F0ap7y%2Fbtra8AiMKmi%2FNLKPKoGi14YCIROcxN6ev1%2Fimg.png)
![[자료구조] 가상 컴퓨터(Virtual machine) 과 시간 복잡도(Time Complexity) - (1)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4ToiJ%2FbtrazMx5Vwj%2F60TNfZ0GDE6sGfoTK88Lz0%2Fimg.png)
![[자료구조] 최초의 알고리즘, 최대 공약수(GCD) 계산 알고리즘, 유클리드 호제법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbKASDj%2Fbtq9GsVdwHb%2FcVz42LWymOkPz8qZbGUEAK%2Fimg.png)