[자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기

목표

피보나치 수열의 시간 복잡도(Time Complexity)에 대해서 이해해보도록 하겠습니다.

 

목차                                                                    클릭하면 해당 목차로 이동합니다.

피보나치(Fibonacci) 수열이란?

 

피보나치 수열을 구하는 알고리즘

 

피보나치 수열 개선하기

 

피보나치 수열 알고리즘을 통한 시간 복잡도 심화

 

정리

 

개요

앞선 포스팅에서 시간 복잡도와 BIG-O 표기법에 대해서 배웠습니다.

이번에는 피보나치 수열의 시간 복잡도를 BIG-O 표기법으로 나타내 보겠습니다. 이를 통해, 어떤 특징이 있는지 알아보겠습니다.

 

피보나치(Fibonacci) 수열이란?

우선, 피보나치 수열이란 첫째 항, 둘째 항이 1이고 그 뒤의 항은 바로 앞의 두 항의 합인 수열을 뜻합니다.

말로 하면 조금 복잡해보이는데요. 직접 예시를 확인해보겠습니다.

F(n) : 1, 1, 2, 3, 5, 8, 13, 21 ····

 

보시면 5번째 항인 5는 앞의 두 항 2, 3의 합과 같습니다. 이런 수열을 피보나치 수열이라고 합니다.

그림으로 쉽게 이해해볼까요?

1항

첫번째 항, 두 번째 항은 1이라고 했습니다. 다음 항을 추가할 때는 정사각형의 모양으로 붙이면 됩니다.

오른쪽으로 2항을 붙여보겠습니다.

2항

그럼 두 개가 붙어서 더 긴 면이 나옵니다. 위나 아래의 길이가 2로 더 길죠? 여기에 하나 다음 항을 붙여보겠습니다.

 

3항

위에 3항인 2를 붙였습니다. 2X2 정사각형 모양으로 다음 항을 붙일 수 있습니다.

이제 왼쪽이나 오른쪽에 길이가 3인 더 긴 면이 있습니다. 다음 항을 또 붙여보겠습니다.

 

4항

3X3의 정사각형을 왼쪽에 붙여서 추가했습니다. 이제 길이가 5인 면을 붙일 수 있겠죠?

5항

점점 거대해지는 기분인데요. 밑에 5X5 정사각형을 추가했습니다.

다음은 길이가 8인 정사각형을 추가할 수 있겠네요.

6항

이렇게 다음 항은 바로 앞의 두 항의 합과 같은 것을 확인할 수가 있습니다.

중심을 보면 다음과 같은 나선형 모양을 확인할 수 있습니다. 기하학의 황금비율인 피보나치의 나선형이라고 합니다.

▲ 피보나치의 나선형, 출처:https://www.youtube.com/watch?v=6Iq5iMCVsXA&t=306s

 

피보나치 수열을 구하는 알고리즘

피보나치 수열을 구하는 알고리즘은 많이 존재합니다. 대부분 재귀함수의 형태로 구현합니다.

재귀함수란, 자기 자신을 다시 호출하는 형태를 띠는 함수입니다. 코드로 확인해보겠습니다.

Fivo(n, r)
{
    if(n<=0)
        return 0
    else if(n==1)
        return r[n] = 1;
    return r[n] = Fivo[n-1, r] - Fivo[n-2,r];
}

다음 항을 알기 위해서는 앞의 두 개의 항을 알아야하기 때문에, n번째 항을 알기 위해 n-1, n-2번째 항을 재귀호출을 합니다.

마찬가지로 그림으로 보면 다음과 같은데요.

▲ 피보나치 수열을 트리모양으로 나타낸 것, 출처:https://www.youtube.com/watch?v=6Iq5iMCVsXA&t=306s

2번씩 트리의 높이 k만큼 반복하는 형태입니다.

그래서 위에 나와 있는 것처럼 시간 복잡도는 O(2^n)입니다.

 

▲ 시간 복잡도 그래프, 출처:https://www.youtube.com/watch?v=6Iq5iMCVsXA&t=306s

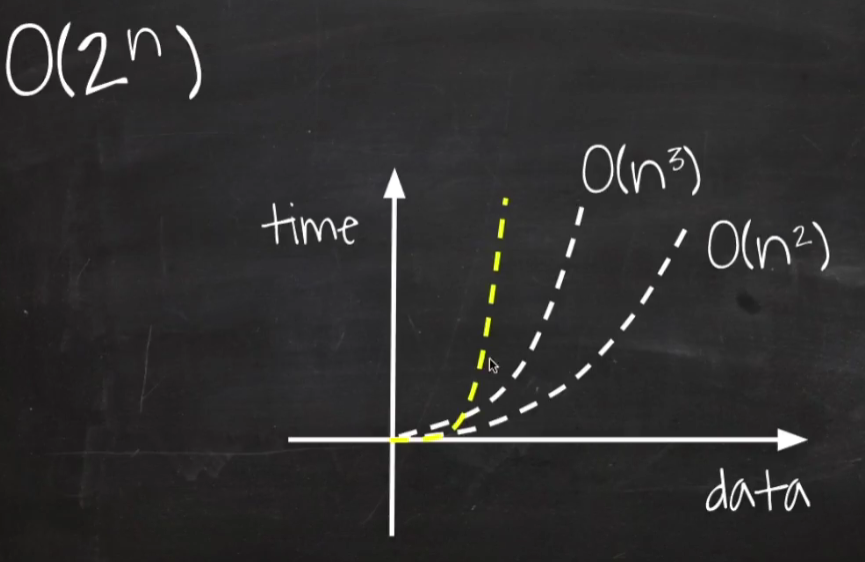
O(n^3)이나 O(n^2)보다도 훨씬 가파르게 상승하는 모습을 확인할 수 있습니다.

알고리즘의 성능이 훨씬 안좋다는 것을 의미합니다.

 

피보나치 수열 알고리즘 개선하기

시간 복잡도로만 봐도 입력 n의 값이 커지면 알고리즘 실행시간이 기하급수적으로 커지는 모습을 확인할 수 있습니다.

효율적인 프로그램을 위해서는 개선이 필요하겠죠? 우선 개선할 수 있는 부분(문제점)을 확인해야 합니다.

위의 트리 형태를 보시면 알겠지만 이전 항들의 값을 가지고 계산하기 때문에 중복되는 부분들이 많습니다.

그만큼 알고리즘의 수행 시간도 길어진다는 것을 의미합니다.

▲ 값이 여러번 중복되는 모습, 출처:https://www.youtube.com/watch?v=VcCkPrGaKrs

위의 사진을 보시면 F(2)만 해도 3번 중복됩니다. F(3)도 2번 중복되고, F(1)이나 F(0)은 더 많이 중복되는 것을 확인할 수 있습니다.

그럼 계산을 진행할 때 앞서 계산한 값을 가지고 있다면 또 함수를 실행하지 않고 값을 가져오기만 하면 되겠죠?

Fivo(n, r)
{
    if(n<=0)
        return 0
    else if(n==1)
        return r[n] = 1;
    else if(r[n]>0) ············ ★
        return r[n]; ··········· ★
    return r[n] = Fivo[n-1, r] - Fivo[n-2,r];
}

이전의 코드에서 별표 친 부분만 추가해줬습니다.

만약, 값을 가지고 있다면 재귀호출을 하지 않고 값만 가져다 주는 것입니다.

 

▲ 중복되는 부분을 제거한 모습, 출처:https://www.youtube.com/watch?v=VcCkPrGaKrs

값을 가지고 있다면, 재귀호출을 하지 않고 값만 반환하기 때문에 노란 부분에서 끝나는 것입니다.

이제 2번씩 반복할 필요가 없기 때문에 시간 복잡도는 O(n)이 됩니다.

입력 n의 값이 커져도 알고리즘의 실행시간이 급격히 증가하지 않겠죠? 성능이 개선되었다고 할 수 있습니다.

 

피보나치 수열 알고리즘을 통한 시간 복잡도 심화

시간 복잡도를 이해하기 위해서 더 비효율적인 코드를 작성하였습니다.

printFivo(n) {
    for(i=1 to n)
        print(Fivo(i))
}

Fivo(n) {
    if(n<=0)
        return 0
    else if(n==1)
        return 1
    return Fivo(n-1) + Fivo(n-2)
}

Fivo(n)은 피보나치 수열의 n번째 항을 확인하는 함수입니다.

printFivo(n)은 피보나치 수열의 첫 번째부터 n번째까지의 항을 출력하는 함수입니다.

보시면 중복된 값들도 계속 재귀호출을 하기 때문에 상당히 비효율적인 것을 알 수 있습니다.

 

이 알고리즘의 시간 복잡도는 어떻게 될까요?

사실 저도 처음엔 O(n*2^n)이라고 생각했습니다. 하지만 그렇지 않습니다.

천천히 보면, printFivo함수는 1부터 n까지 Fivo함수를 호출합니다. 그럼 이걸 2^1 , 2^2 ··· 2^n까지 호출하게 됩니다. 

이걸 다 더해주면 시간 복잡도가 나오게 됩니다. 보기 좋게 적으면 다음과 같습니다.

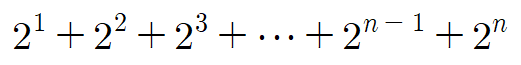
가만히 보면 첫 항이 2이고, 공비가 2인 등비수열임을 알 수 있습니다.

등비수열의 공식에 대입하면 시간 복잡도 T(n) = 2^(n+1) -2 입니다.

 

제가 보는 영상에서 알려준 게, 마지막 항 2^n 앞에까지 더한 것은 2^n-2와 같다고 합니다.

한번 확인해볼까요?

2^1 + 2^2 + 2^3 + 2^4 를 풀어서 쓰면 " 2 + 4 + 8 + 16 " 이 됩니다.

마지막 16을 빼고 2+4+8= 14 입니다. 정말 마지막항 16에서 2를 뺀 값인 14가 되네요.

 

과정이 어찌 되든 결과는 T(n) = 2^(n+1)-2 입니다.

그럼 BIG-O 표기법으로 나타내면 어떻게 될까요?

최고차항을 뺀 나머지 항을 생략하고 최고차항의 계수를 생략해서 나타내야 합니다.

그럼 결국 2^n만 남게 됩니다. 따라서 시간 복잡도는 BIG-O로 나타내면 O(2^n)입니다.

 

제가 비효율적인 코드를 작성한다고 했는데, 사실 BIG-O로 확인해보면 큰 차이 없었습니다.

 

정리

시간 복잡도 강의를 유튜브로 보다 보니 관련 영상에 떠서 봤는데 설명을 너무 잘해주셔서 글로 옮겼습니다.

좋은 영상 감사드립니다!

 

시간 복잡도에 대한 개념은 크게 어려운 것 같진 않지만 막상 알고리즘을 보면서 생각해보면 헷갈리는 부분이 꽤 많은 것 같습니다. 놓치기 쉬워 신경 써야 하는 부분도 꽤 있는 것 같습니다. 틈틈이 확인하면서 까먹지 않도록 해야겠습니다.

 

이제 알고리즘 성능 평가를 위한 시간 복잡도에 대한 내용은 마무리하고 다양한 자료구조에 대해서 알아보도록 하겠습니다.

 

출처 :유튜브 엔지니어 대한민국 https://www.youtube.com/watch?v=VcCkPrGaKrs