![[자료구조] 최초의 알고리즘, 최대 공약수(GCD) 계산 알고리즘, 유클리드 호제법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbKASDj%2Fbtq9GsVdwHb%2FcVz42LWymOkPz8qZbGUEAK%2Fimg.png)

목표
인류 최초의 알고리즘인 최대 공약수를 구하는 알고리즘에 대해 알아보도록 하겠습니다.
목차 클릭하면 해당 목차로 이동합니다.
개요
다음 학기에 배울 알고리즘을 준비하기 위해 자료구조를 복습하기로 했습니다.
이번 포스팅에서는 최초의 알고리즘인 최대 공약수를 구하는 알고리즘에 대해 알아보도록 하겠습니다.
알고리즘(Algorithm)의 어원
9세기에 현재 이란, 이라크 지역인 페르시아에서 대수학에 재능이 있던 수학자가 있었습니다.
"알 - 카와리즈미(Al-khwarizmi)" 라는 수학자인데, 대수와 0에 관한 책을 페르시아어로 썼습니다.
이 책이 번역되서 유럽에 라틴어로 넘어가는 과정에서 "Algorismus"로 번역되서 넘어갔습니다.
수에 관한 책이니까 라틴어로 수라는 뜻의 Arithmos 라는 이름이 붙어서 유럽으로 넘어가게 됩니다.
Algorismus + Arithmos 이렇게 넘어가게 되는데, 여기서 일부분을 떼서 Algorismus + Arithmos 해서
Algorithm(알고리즘)이라는 말이 만들어지게 됩니다.
최대 공약수(GCD) 계산 알고리즘, 유클리드 호제법
최초의 알고리즘은 유클리드(Euclid)가 만든 두 수의 최대 공약수 알고리즘입니다.
큰 수에서 작은 수를 빼서 한 개의 수가 0이 될 때까지 계산을 계속하는 것입니다.
예를 들어, GCD(8,12) = max{1, 2, 4} = 4 인 것을 다들 아실 것이라고 생각하는데요.
어떤 원리로 이렇게 되는걸까요?
원리는 큰 수에서 작은 수를 계속 빼서 같은 수가 나올 때까지 반복하는 것입니다.
다음을 보면, 12(4X3)와 8(4X2)을 아래와 같이 표현할 수 있습니다.

큰 수(12)에서 작은 수(8)을 빼면 4가 남고 오른쪽과 같이 되는겁니다.

다시 한 번 큰 수(8)에서 작은 수(4)를 빼면 4가 되고, 한번 더 과정을 반복하면 4와 0이 남게 됩니다.
이렇게 GCD(최대 공약수)는 4라는 것을 알 수 있습니다.
이 과정을 코드로 나타내면 다음과 같이됩니다.
gcd(a, b):
while a!=0 and b!=0:
if a > b:
a = a - b
else:
b = b - a
return a + b두 수가 둘 다 0이 아니라면 수를 비교해서 값을 바꾸는 것입니다.
a, b 중에 큰 수(0이 아닌 수)를 반환해야할 것 같은데 return a+b 라고 적었습니다.
그 이유는 둘 중 하나는 무조건 0이기 때문에 가능한 것입니다.
이를 GCD_SUB 라고 표현합니다.
하지만, 만약 GCD(2,100) 이라면 반복문을 50번이나 반복해야합니다.
이 때, 뺄셈을 나머지 연산(modulo, %)으로 바꾼다면 반복문 실행 횟수를 줄일 수 있습니다.
gcd(a, b):
while a!=0 and b!=0:
if a > b:
a = a % b
else:
b = b % a
return a + b이와 같이 모듈러(%)를 사용하면 반복문 실행 횟수가 줄일 수 있습니다.
이 외에도 GCD_REC 이라고 해서, GCD를 재귀함수를 이용해서 계산하는 것입니다.
GCD(a,b) = GCD(a, b%a) 혹은 GCD(a%b, b) 처럼 재귀함수를 사용해서 GCD를 구할 수 있습니다.
gcd(a,b):
if(a != 0 and b != 0):
if(a > b):
return gcd(a%b, b)
else:
return gcd(a, b%a)
return a + b이렇게 재귀함수를 이용해서도 구할 수 있습니다.
반복문은 없지만, 계속 함수를 실행해야하기 때문에 overhead가 발생하겠죠?
얼마나 많은 overhead가 발생하는지는 함수를 몇번 호출하냐에 달려 있습니다.
저는 GCD_MOD의 반복문 실행 횟수와 함수 호출 횟수가 같다고 예상하는데 맞는지 확인해보도록 하겠습니다.
GCD를 파이썬으로 구현하기
우선 GCD_SUB부터 작성해보도록 하겠습니다.

위와 같이 작성했고, cnt는 반복문이 몇 번 돌아가는지 확인하기 위해 추가한 변수입니다.
뺄셈을 그대로 모듈러 연산자로 바꿔서 GCD_MOD를 작성하겠습니다.
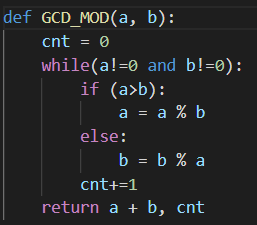
그대로 연산자만 바꿔서 작성한 것을 확인할 수 있습니다.
다음은 GCD_REC을 작성해보도록 하겠습니다.

이렇게 세 개의 함수를 정의해놓고 실행해보도록 하겠습니다.
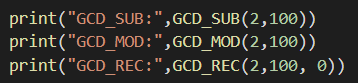
GCD_REC의 세번째 인자 0 은 cnt 를 0부터 시작하기 위해 추가해준 것입니다.
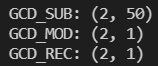
위처럼 결과가 나왔습니다. (결과, 실행횟수) 입니다.
세 개 다 GCD(2,100)을 실행했기 때문에 최대 공약수 2가 앞에 나왔습니다.
GCD_SUB는 반복문을 50번 돌았고, MOD는 1번, REC도 1번만 함수를 호출한 것을 확인 할 수 있었습니다.
정리
이렇게 최초의 알고리즘인 유클리드 호제법, 최대 공약수 구하는 알고리즘에 대해서 알아보았습니다.
내용 자체는 중학교 과정에서 배우는 내용이기 때문에 낯설지 않습니다.
이 내용을 이렇게까지 다루는 것은 유클리드 호제법에 대해서 알기 위함도 있지만 중요한 것은 알고리즘은 생각보다 단순한 것이라는 것을 깨닫기 위함입니다. 어렵다고 생각하면 끝도 없는게 알고리즘이라고 생각합니다.
앞으로 다양한 알고리즘과 자료구조를 다루면서 절망도 많이 하고 벽도 느낄 텐데, 그 때마다 이 글을 보면서 천천히 다시 생각하는 마음가짐을 다잡을 수 있을거라고 기대하고 있습니다.
*한국외대 신찬수 교수님의 Data Structures with Python 강의를 참고하여 포스팅하였습니다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 순차적 자료구조, 배열과 리스트의 이해 (0) | 2021.08.10 |
|---|---|
| [자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기 (1) | 2021.08.03 |
| [자료구조] 시간 복잡도를 나타내는 BIG-O 표기법 - (3) (0) | 2021.08.02 |
| [자료구조] 알고리즘 성능평가를 위한 시간 복잡도 완벽히 이해하기! - (2) (1) | 2021.07.28 |
| [자료구조] 가상 컴퓨터(Virtual machine) 과 시간 복잡도(Time Complexity) - (1) (0) | 2021.07.26 |
![[자료구조] 피보나치 수열의 시간 복잡도 완벽히 이해하기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fd5OYJm%2FbtraWvwiTlx%2F6k2TReYFOkcHGhkTM6np90%2Fimg.png)
![[자료구조] 시간 복잡도를 나타내는 BIG-O 표기법 - (3)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F0ap7y%2Fbtra8AiMKmi%2FNLKPKoGi14YCIROcxN6ev1%2Fimg.png)
![[자료구조] 알고리즘 성능평가를 위한 시간 복잡도 완벽히 이해하기! - (2)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcwjCNA%2FbtraGG6gLWI%2FQR6ZXbskiELd3CV9dHK5K1%2Fimg.png)
![[자료구조] 가상 컴퓨터(Virtual machine) 과 시간 복잡도(Time Complexity) - (1)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4ToiJ%2FbtrazMx5Vwj%2F60TNfZ0GDE6sGfoTK88Lz0%2Fimg.png)